| Kurzus | Matematika kémikusoknak I. | Kód | K011 | ||||
| Szak | (vegyész, klinikai kémikus, kémiatanár kötelező) | Kredit | 4 | ||||
| Felelős oktató |
Dr. Horváth István
egyetemi docens |
Számonkérés | K5 | ||||
| Létszámkorlát | 100 fő | ||||||
| Típus | előadás | Heti óraszám | 4 | Periódus | őszi félév | Javasolt félév | 1. (mintatanterv) |
| Előfeltétel | nincs | ||||||
| Teljesítés feltétele | Matematika gyakorlat kémikusoknak I., K012 párhuzamos felvétele | ||||||
| Helyettesítő tárgy | Egyváltozós függvények differenciálása, M105 és Egyváltozós függvények integrálása, M232 kreditek | ||||||
Tematika:
Valós számfogalom felépítése. Műveletek a komplex számkörben.
Műveletek vektorokkal, vektorterek.
A határérték fogalma, műveletek konvergens sorozatokkal.
A határérték és az egyenlőtlenség kapcsolata, konvergencia-kritériumok.
Az e szám bevezetése.
Függvények folytonosságának definíciója, a szakadások
fajai. Zárt intervallumon folytonos függvények tulajdonságai. Az inverz
függvény definíciója és tulajdonságai. A hatvány függvény definíciója és
tulajdonságai. Az exponenciális függvény definíciója és tulajdonságai.
A logaritmus függvény definíciója és tulajdonságai. A sin x függvény definíciója
és tulajdonságai. A cos x függvény definíciója és tulajdonságai. A tg x
és ctg x definíciója függvények és tulajdonságaik. A ciklometrikus függvények
definíciója és tulajdonságaik.
A differenciálhányados definíciója, a műveletek és a differenciálás
kapcsolata. A differenciálszámítás középérték tételei. A L'Hospital-szabály.
A lokális szélsőérték, a növekedés és fogyás feltételei. Az inflexiós pont,
a konvexitás és konkávitás feltételei. A függvényvizsgálat általános menete.
A Taylor-polinom és maradéktagjai. Komplex tagú sorok.
A határozott integrál definíciója és tulajdonságai.
A parciális integrálás módszere. A helyettesítéssel történő integrálás
módszere. Racionális törtfüggvények integrálása elemi törtekre bontással.
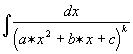 típusú integrálok.
típusú integrálok. ![]() dx
és
dx
és ![]() dx típusú
integrálok.
dx típusú
integrálok.
 dx típusú integrálok.
dx típusú integrálok. ![]() dx
típusú integrálok.
dx
típusú integrálok.
![]() dx típusú integrálok.
dx típusú integrálok.
Az imprópriusz integrálok definíciója és kiszámításuk.
Mutasson be példákat az integrálszámítás geometriai alkalmazására. Közelítő
integrálás
Irodalom:
- Huhn Péter: Matematika vegyészeknek I.–II. JATE Kiadó Szeged 1990.
- Leindler László: Analízis, JATE Kiadó, Szeged
- Dancs István (szerk): Bevezetés a matematikai analízisbe, Aula Kiadó
- További matematikai analízis jegyzetek és tankönyvek.